Ampere's law and the e/m experiment
Moving charged particles produce magnetic fields and are acted on by magnetic
fields. Currents are moving charges and therefore they produce and are
acted on by magnetic fields. Permanent magnets are the result of
"magnetization currents" flowing inside the material.
In experiment 1 of this lab you will use a compass needle to measure the
magnetic field produced by a current-carrying wire.
In experiment 2 of this lab you will observe the deflection of electrons in a
magnetic field and use this deflection to determine the electron's charge to
mass ratio.
Equipment Needed:
- e/m Apparatus
- Pasco Low Voltage Power Supply
- Patch cords
- Magnet
- Compass needle
Open a Microsoft Word document to keep a log of your experimental procedures,
results and discussions. This log will become your lab report. Address the
points highlighted in blue. Answer all questions.
Currents produce magnetic fields and current-carrying wires are deflected in
magnetic field.
Experiment 1
 Use the "Low Voltage" power supply. Before you turn
it on, turn the voltage knob all the way up (clockwise) and the current knob all the way
down (couterclockwise). After you have connected a load, you can then control the current
passing through the load by slowly turning the current knob
clockwise.
Use the "Low Voltage" power supply. Before you turn
it on, turn the voltage knob all the way up (clockwise) and the current knob all the way
down (couterclockwise). After you have connected a load, you can then control the current
passing through the load by slowly turning the current knob
clockwise.
(a) Let the wire cross the needle at right angle as shown.

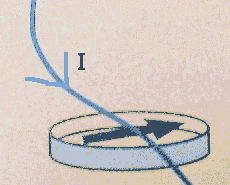
Slowly turn up the current to ~ 3 A.
Do you see any deflection of the needle?
Turn the current back down before the wire gets hot.
Record your observation. Is the needle
deflected? Do you expect a deflection? Why or why
not?
Switch the direction of the current flow by
switching the red and black lead at the power supply.
Record your observation. Is the needle
deflected? Do you expect a deflection? Why or why
not?
(b) Now align the wire with the needle.


Let the current pass over the needle from North to South.
Slowly turn up the current to ~ 3 A. Do you see any
deflection of the needle? T
urn the current back down before the wire gets
hot.
Record your observation. Is the needle deflected?
Do you expect a deflection? Why or why not?
Let the current pass over the needle from South to North and
repeat.
What do you see? Can you explain
your observation?
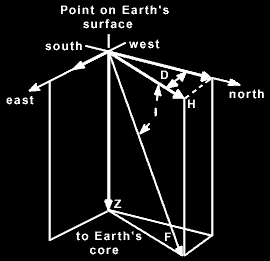
 Near Knoxville, TN, the strength
of the Earth magnetic field is ~ 53 microT. It has a declination D
(deviation from North) of about 3o and an inclination I
(downward tilt) of ~ 65o, so its horizontal component has a
magnitude of approximately 53 microT*cos(65o) = 22 microT.
Near Knoxville, TN, the strength
of the Earth magnetic field is ~ 53 microT. It has a declination D
(deviation from North) of about 3o and an inclination I
(downward tilt) of ~ 65o, so its horizontal component has a
magnitude of approximately 53 microT*cos(65o) = 22 microT.
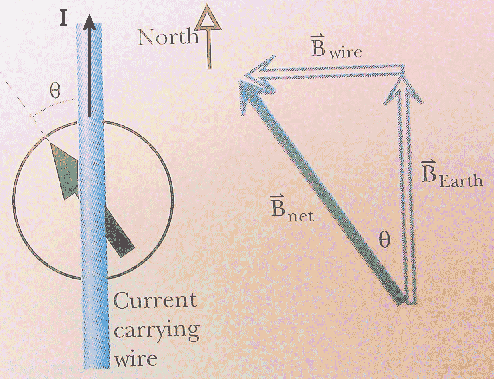
The magnetic field of the wire and the Earth magnetic field
are vectors and add vectorially. If the wire is aligned with the compass
needle when no current flows through the wire, and the magnitude of average field due to the wire at the compass needle
is approximately equal to magnitude of the horizontal component of the Earth field, you should see a
deflection of ~45o.
Can you deflect the needle by ~ 45o with a current of less than 4 A? Would you expect to be able to?
What current do you need to produce a magnetic field of magnitude 22 microT
at a distance of the needle from the wire?
(Review: The
magnetic field produced by a steady current flowing in a long straight
wire)
Activity 1
Magnetic fields exert forces on other moving charge. The force a magnetic field exerts on a charge q, moving
with velocity v, is called the
Lorentz force.
It is given by F = qv × B.
Assume a charged particle is
moving with velocity v through a region with magnetic field
B.
Predict the direction of the magnetic force for each
situation below. Assume that the particle is positively charged.
Record your predictions in your log.
(a)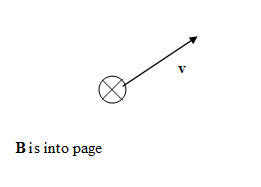 (b)
(b)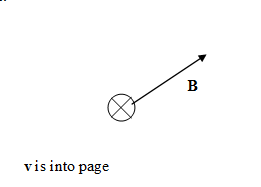
(c)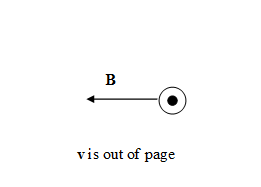 (d)
(d)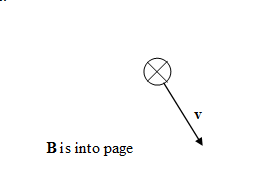
Experiment 2
Part 1: Measuring e/m
Mass spectrometry has become an important
measurement tool in clinical chemistry, microbiology, toxicology and in the
pharmaceutical world. A mass spectrometer deflects ionized and accelerated
molecular fragments using a magnetic field and sorts them according to their
charge to mass ratio. For this exercise you will use
an e/m apparatus like a mass spectrometer to determine the electron's
charge to mass ratio, e/m, by measuring the radius of curvature of an electron's
path in a uniform magnetic field of known strength.
You will use the "Fine Beam Tube System" show below. All
components are labeled.

Inside a glass tube a beam of electrons is
accelerated through a known potential difference, so the kinetic energy
and therefore the velocity of the electrons is known. A pair of
Helmholtz coils can produce a uniform magnetic field at right angles to
the electron beam. This magnetic field then deflects the electron
beam in a circular path. The diameter of this circular path can be
measured using the calibration marks in the center of the tube, which are
equally spaced by 2 cm.
The glass tube is filled with helium at a low pressure of 13 Pa. It
contains an electron gun and an electrostatic lens (Wehnelt) system. A heater heats
the cathode, which emits electrons. The electrons are accelerated by a
potential difference between the cathode and the anode. The electron beam
leaves a visible trail in the tube, because some of the electrons collide with
helium atoms. The atoms are excited and then radiate visible light.
The tube socket rotates, allowing the electron beam to be oriented at any
angle (from -10 to 270 degrees) with respect to the magnetic field produced by
the Helmholtz coils. The vector nature of the magnetic force on
moving charged particles can therefore be explored. A small
permanent magnet can also be used to deflect the electron beam.
In order to rotate the tube, loosen the screw, but do not screw it all the
way out. Do not turn the tube itself, instead rotate the turntable.
then tighten the screw again.

The radius of the Helmholtz coils is equal to their separation.
This geometry provides a highly uniform magnetic field near the center
of the coils. The Helmholtz coils of the apparatus have
a radius and a separation of ~15 cm. Each coil has 124 turns.
The magnetic field B produced by the coils is proportional to the
current I through the coils times 7.56*10-4 T/A. It is
perpendicular to the plane of the coils.
B = (7.56*10-4 T/A)*I.
Analysis of an e/m measurement
The magnetic force Fm acting on a charged particle of
charge q moving with velocity v in a magnetic field B is given by
the equation
F = qv × B.
If the electron beam velocity is perpendicular to the magnetic field, we have
the following equation relating the magnitudes Fm, q, v, and B.
Fm = qvB.
The electron is moving in a circular path of radius r, with the magnetic
force being equal to the centripetal force mv2/r. We therefore have
qvB = mv2/r or q/m = v/Br.
We denote the magnitude of the charge qe of the electron by e and therefore
have e/m = v/Br.
The electrons are accelerated by the accelerating potential V, gaining kinetic
energy equal to their charge times the accelerating potential.
Therefore eV = ½mv2.
The velocity of the electrons is v = (2eV/m)½. Inserting this
expression for v in the equation above and squaring both sides we obtain
e/m = 2V/(Br)2 or 2V = (e/m) (Br)2.
The slope of a plot of 2V versus (Br)2 is equal to electron charge
to mass ration e/m.
Procedure
- Align the tube as shown in the picture above, with the electron gun
perpendicular to the with the magnetic field produced by the Helmholtz
coils. Then turn the power supply on and work in a darkened room.
- Set the adjustment knob for the heater voltage to a position in the middle (~6V).
- Turn the knob for the coil current all the way to the left (0 A).
- Wait about a minute for the heater temperature to stabilize. Then
slowly increase the anode voltage to 300 V. The electron beam path
will become visible.
- Select the Wehnelt voltage so that the electron beam is narrow and
clear. Optimize the focus and brightness of the beam by varying the
heater voltage.
- Increase the coil current until the electrons move in a circle of radius
r = 4 cm or diameter 8 cm. (Take some time to adjust the current
carefully. Remember that the calibration marks in the center of the tube are
equally spaced by 2 cm. Place your eye so that the front and back
calibration marks line up and the electron beam passes in between.)
- Paste the table below into an Excel spreadsheet and enter your measured
value for the coil current into the table.
- Repeat for the other accelerating voltages in the table. (Fill the
table from the bottom up.)
- Let Excel calculate the remaining columns in the table.
- Produce a graph of 2V versus(Br)2 and label the axes.
- Add a trendline, set the intercept to zero, and display the equation on
the chart. Format the trendline label Scientific, 2 decimal places.
Accelerating
voltage
(V) |
Current
to coils
I (A) |
Magnetic field
B =
(7.56*10-4 T/A)*I |
Radius of
circular path
r (m) |
(Br)2
(units: T2m2) |
2V
(units: J/C) |
|
200 |
|
|
0.04 |
|
|
|
220 |
|
|
0.04 |
|
|
|
240 |
|
|
0.04 |
|
|
|
260 |
|
|
0.04 |
|
|
|
280 |
|
|
0.04 |
|
|
|
300 |
|
|
0.04 |
|
|
-
Insert your table and your graph into your Word document.
-
What is the slope of your trendline? (Note: The
slope will have units (J/C)/(Tm)2 = C/kg.)
-
What is your measured value of e/m?
-
Calculate e/m from the
accepted values of the
electron's charge and mass. Does the value of e/m from your experiment agree
with the calculated value? Given your experimental procedure, how close do you
expect them to agree?
Part 2: Electrons moving in a magnetic field
Procedure:
The socket for the e/m tube is designed so that the tube can be rotated. By setting up the equipment as for measuring e/m, you can
rotate the tube and study how the beam deflection is affected.
Rotate the tube up to ~ 10o to either side.
- Describe your observations as you rotate the tube.
- Describe what happens when you change the current to the Helmholtz
coils.
- Describe what happens when you change the accelerating voltage.
Instead of using the Helmholtz coils to bend the electron beam, you can
use a permanent magnet to show the effect of a magnetic field on the
electron beam. Set the acceleration potential to 300 V and the Helmholtz coil current
to 0.
- When the electron beam appears, use a permanent magnet to bend
the beam.
- Describe your observations as you bring the north pole of your
magnet close to the beam.
- Describe your observations as you bring the south pole of your
magnet close to the beam.
Convert your log into a lab report.
See the grading scheme for all lab
reports.
Name:
E-mail address:
Laboratory 4 Report
- In one or two sentences, state the goal of this lab.
- Make sure you completed the entire lab and answered all parts. Make
sure you show your work and inserted and properly labeled relevant tables
and plots.
- Add a reflection at the end of your report in a short essay format.
Save your Word document (your name_lab4.docx), go to Canvas, Assignments, Lab
4, and submit your document.
 Use the "Low Voltage" power supply. Before you turn
it on, turn the voltage knob all the way up (clockwise) and the current knob all the way
down (couterclockwise). After you have connected a load, you can then control the current
passing through the load by slowly turning the current knob
clockwise.
Use the "Low Voltage" power supply. Before you turn
it on, turn the voltage knob all the way up (clockwise) and the current knob all the way
down (couterclockwise). After you have connected a load, you can then control the current
passing through the load by slowly turning the current knob
clockwise.


 Near Knoxville, TN, the strength
of the Earth magnetic field is ~ 53 microT. It has a declination D
(deviation from North) of about 3o and an inclination I
(downward tilt) of ~ 65o, so its horizontal component has a
magnitude of approximately 53 microT*cos(65o) = 22 microT.
Near Knoxville, TN, the strength
of the Earth magnetic field is ~ 53 microT. It has a declination D
(deviation from North) of about 3o and an inclination I
(downward tilt) of ~ 65o, so its horizontal component has a
magnitude of approximately 53 microT*cos(65o) = 22 microT.
 (b)
(b)
 (d)
(d)

